The Advent of Code is an annual programming competition with a lot of interesting puzzles. While the competition is mostly about answering the questions as quickly as possible, I instead prefer to challenge myself to come up with low-latency solutions for each problem. Now that the 2023 edition of AOC is wrapped up, I thought it would be interesting to go into a bit of detail about some of the faster and more unique solutions that I came up with.

This post will contain spoilers for both problems and solutions for AOC 2023. If you’re thinking about solving these problems yourself at some point in the future, I’d recommend closing this page and coming back after you’re done. One of the most fun aspects of AOC is not knowing what’s coming next.

Originally, my goal for this post was to complete all 50 parts in under 100 milliseconds. The goal was in sight until day 23 threw an NP-hard problem at us. While it’s certainly possible to fully optimize solutions for all days and reach the sub-100ms mark, 25 days of puzzling has me tired enough that I’d rather focus on more interesting solutions to some of the earlier problems. There was a lot of room for clever optimization in this year’s round of puzzles, and I think there’s a lot to be learned from looking at some of the more performant solutions.

I’m working on improving my Rust at the moment, so all solutions this year will be presented in Rust.

First, a few disclaimers:

• None of these solutions have been micro-optimized; there is almost certainly a lot of potential performance left on the table as a result. There are certainly even faster solutions possible for each problem than I will present here
• One of the interesting parts of AOC is that your input is part of the problem statement. Solutions do not have to be correct for all possible inputs to be correct for AOC. This means that some of the solutions presented rely on properties of my input specifically and may not provide correct answers for arbitrary inputs!
• All benchmarks are run on a 2022 Framework laptop running Ubuntu with stock kernel/OS configuration

This post ended up being much longer than I was originally intending. If you don’t want to read the whole thing, day 10 and day 16 are probably the most interesting.

With all of that out of the way, let’s get into it!

A note on AI programming assistants 🔗

The primary reason that I participate in AOC every year is to solve fun problems by exercising my engineering skills. Asking an AI assistant to solve problems for me doesn’t help with that. As such, ChatGPT and friends were not used to write any of the code that I’ll be writing about. That being said, I did allow myself two concessions:

• Copilot is fair game as intelligent auto-complete. It’s a tool I use in day-to-day programming, and I generally find it very useful. I don’t see any reason to waste time manually typing in point translation code that Copilot can reliably auto-complete for me
• I allowed myself to use ChatGPT to discover new data structures/algorithms. This means that questions like “What algorithms can be used to determine if a Cartesian point lies within a given polygon?” are fair game, but entering the text of a problem or problem-specific details are not. This turned out to be a fantastic use of the tool, as it was able to provide me with Wikipedia links to algorithms 100% of the time that I decided to use it. This was much more useful than I’ve found Googling to be for this type of query in the past

General approach 🔗

My approach to achieve low-latency solutions for these types of problems relies mostly on mechanical sympathy:

• Exploit cache locality; ideally, never leave L1 cache
• Minimize allocations; ideally, don’t dynamically allocate at all
• Maximize pipeline throughput by avoiding branches; ideally, no branches at all
• Eliminate shared mutability to enable parallelism
• Minimize the time complexity of the algorithm

Generally, I’m looking to apply these concepts in order; that is, if I have to choose between making a dynamic allocation or exceeding L1 cache, I’ll prefer to perform the allocation and stay within the L1 cache range. Importantly, this means that time complexity is the last consideration that I’m making. This might seem strange, but the nature of modern processors is such that making proper use of the hardware is usually far more impactful to latency than the total number of operations performed.

These concepts are too deep to explain properly in this post, but one canonical example that we’ll see come about in a few of my solutions is use of a Vec where one might expect to see a HashMap. The amortized time complexity of HashMap operations is O(1), while most of the corresponding Vec operations are O(N) or O(log(N)) at best. Theoretically speaking, HashMap should be faster because it’s performing many less operations. In reality, for small N (as is often the case in these problems), the locality properties of Vec dominate the number of operations. In conversation with others, it wasn’t rare to see them achieve a 10-50% speed-up in their solution simply by swapping out their HashMaps.

So, the goal is to solve the problems while taking maximal advantage of L1 cache, avoiding allocations, avoiding branches, avoiding shared mutability, then finally minimizing total number of operations.

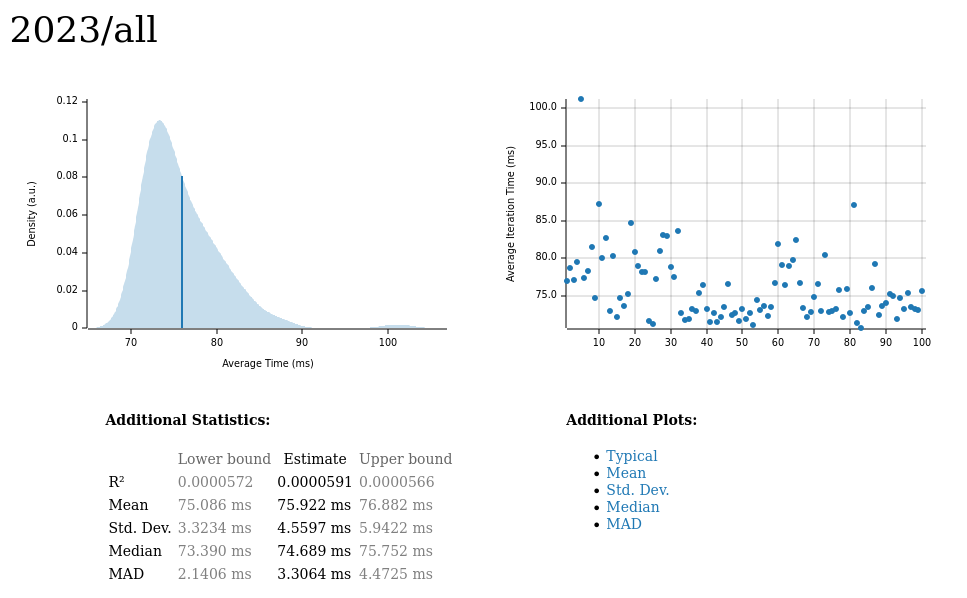
Criterion reports 🔗

Each solution includes a Criterion benchmark showing the total latency for parsing the problem input and solving both parts. The reports will look like this:

The plot on the left displays the average time per iteration for this benchmark. The shaded region shows the estimated probability of an iteration taking a certain amount of time, while the line shows the mean.

The plot on the right shows the linear regression calculated from the measurements. Each point represents a sample, though here it shows the total time for the sample rather than time per iteration. The line is the line of best fit for these measurements.

Since the example here is the total latency of all solutions, there is a high variance in the measurements, resulting in a poor best fit line. The individual solutions are more deterministic as you will see later.

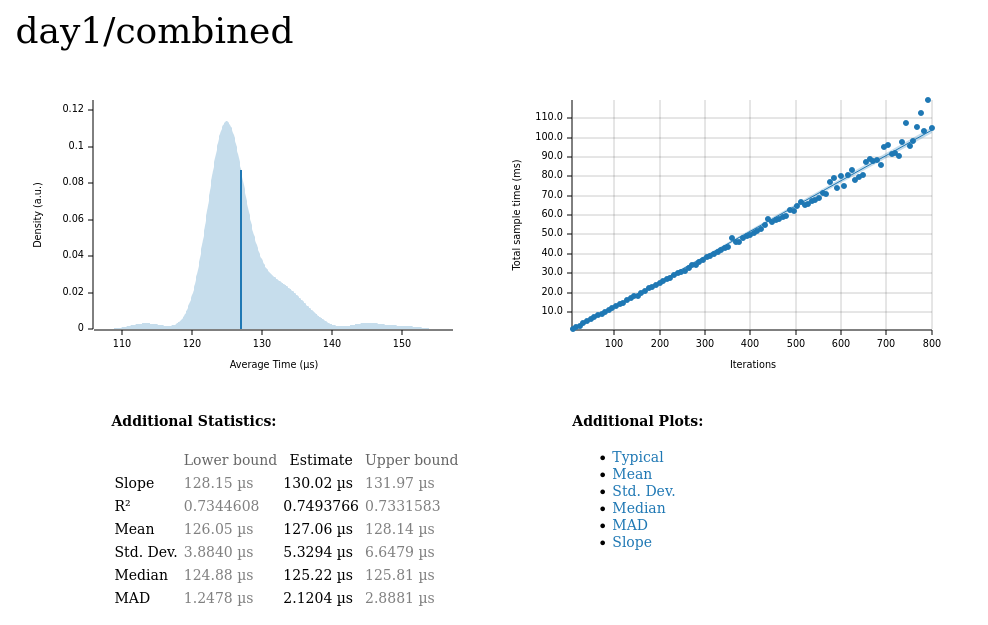
Day 1 🔗

Total input size: ~22,000 characters
Median latency: 125μs

Solution on GitHub

The first problem of the year was to calculate the sum of the first and last digit on each line of input. Input for the problem looks like:

1abc2
pqr3stu8vwx
a1b2c3d4e5f
treb7uchet

This can be achieved with no allocation or backtracking on a single pass through the input data, though a branch is required. The trick is to realize that there is only ever a single state to care about for each line: no digits have been seen, a single digit has been seen, or more than one digit has been seen. The state is updated as new digits are encountered, and when a newline is encountered, the total sum is updated using the final value that can be generated from the current state. Updating the sum also resets the state so that it’s ready for re-use on the next line.

Another potential approach is to scan once from the beginning of each line for the first digit, then once from the end for the second; however, this approach requires two passes through the input (the first to identify the line boundaries, and the second to run the actual scanning logic).

enum State {
    Empty,
    SingleDigit(u32),
    DoubleDigit(u32, u32),
}

impl Default for State {
    fn default() -> Self {
        Self::Empty
    }
}

impl State {
    pub fn update(self, val: u32) -> Self {
        match self {
            Self::Empty => Self::SingleDigit(val),
            Self::SingleDigit(a) => Self::DoubleDigit(a, val),
            Self::DoubleDigit(a, _) => Self::DoubleDigit(a, val),
        }
    }

    pub fn extract(self) -> u32 {
        match self {
            Self::SingleDigit(a) => a * 10 + a,
            Self::DoubleDigit(a, b) => a * 10 + b,
            _ => panic!("Invalid input, attempted to extract from empty state"),
        }
    }
}

#[aoc(day1, part1)]
pub fn trebuchet_simple(input: &str) -> u32 {
    let mut result = 0u32;
    let mut state = State::default();
    let mut chars = input.chars();
    while let Some(ch) = chars.next() {
        if let Some(digit) = ch.to_digit(10) {
            state = state.update(digit);
        } else if ch == '\n' {
            result += state.extract();
            state = State::default();
        }
    }
    result + state.extract()
}

Part 2 extends the problem so that not only digits have to be parsed, but English representations of each digit is fair game as well. The input now looks like:

two1nine
eightwothree
abcone2threexyz
xtwone3four
4nineeightseven2
zoneight234
7pqrstsixteen

With a minor amount of duplication, the solution is nearly the same. We’re now forced to perform a look-ahead at each character to check if a word can be parsed. The index of the word in the WORDS array is re-used as its value for the resulting sum, meaning that no additional mapping or parsing is required.

For this part, the “per-line scan” I mentioned previously seems to be faster than my approach due to the backtracking.

const WORDS: [&str; 9] = [
    "one", "two", "three", "four", "five", "six", "seven", "eight", "nine",
];

#[aoc(day1, part2)]
pub fn trebuchet_wordy(input: &str) -> u32 {
    let mut result = 0u32;
    let mut state = State::default();
    let mut chars = input.chars();
    let mut ch: Option<char>;
    while {
        let mut digit = 1;
        for word in WORDS {
            if chars.as_str().starts_with(word) {
                state = state.update(digit);
                for _ in 0..word.len() - 2 {
                    chars.next();
                }
                break;
            }
            digit += 1;
        }
        ch = chars.next();
        ch.is_some()
    } {
        if let Some(digit) = ch.unwrap().to_digit(10) {
            state = state.update(digit);
        } else if ch.unwrap() == '\n' {
            result += state.extract();
            state = State::default();
        }
    }
    result + state.extract()
}

The results:

We can see that even for a relatively simple problem like this one, trying to squeeze performance out of the solution requires thinking about the problem in a slightly different way than usual.

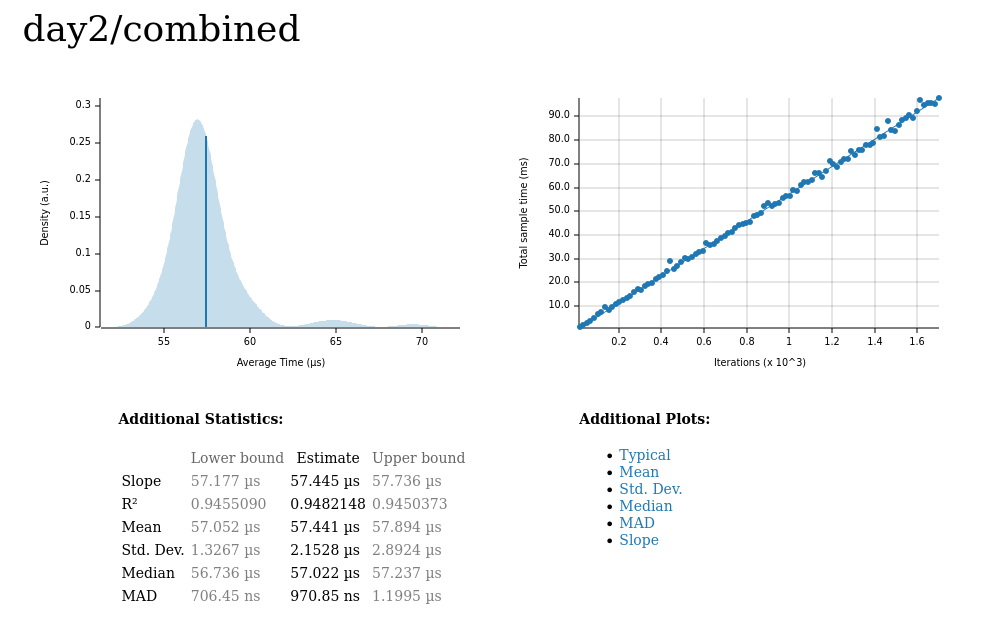
Day 2 🔗

Total input size: 100 scenarios, ~10,500 characters
Median latency: 56μs

Solution on GitHub

The day 2 problem was to answer some questions about a set of games played with cubes. Cubes are removed from a bag a number of times; the input shows you the results of each removal separated by a ;. Cubes are returned to the bag after being removed. The problem input looks like:

Game 1: 3 blue, 4 red; 1 red, 2 green, 6 blue; 2 green
Game 2: 1 blue, 2 green; 3 green, 4 blue, 1 red; 1 green, 1 blue
Game 3: 8 green, 6 blue, 20 red; 5 blue, 4 red, 13 green; 5 green, 1 red
Game 4: 1 green, 3 red, 6 blue; 3 green, 6 red; 3 green, 15 blue, 14 red
Game 5: 6 red, 1 blue, 3 green; 2 blue, 1 red, 2 green

For part 1, we must determine which games would have been possible if the bag contained exactly 12 red cubes, 13 green cubes, and 14 blue cubes.

Almost all of the time for this solution is spent parsing the input:

#[derive(Default)]
pub struct Round {
    red: u32,
    green: u32,
    blue: u32,
}

pub struct Game {
    rounds: Vec<Round>,
}

#[aoc_generator(day2)]
pub fn generate(input: &str) -> Vec<Game> {
    input
        .lines()
        .map(|line| Game {
            rounds: line
                .split(": ")
                .skip(1)
                .next()
                .unwrap()
                .split("; ")
                .map(|round| {
                    let mut res = Round::default();
                    for color in round.split(", ") {
                        let mut it = color.split(" ");
                        let num = u32::from_str_radix(it.next().unwrap(), 10).unwrap();
                        match it.next().unwrap() {
                            "red" => res.red = num,
                            "blue" => res.blue = num,
                            "green" => res.green = num,
                            _ => panic!(),
                        }
                    }
                    res
                })
                .collect(),
        })
        .collect()
}

We step through each line, parsing each Round into a Game. Rust’s Iterator make this very simple. The solution to part 1 is also straightforward: a game is possible only if the maximum value seen for each color is exactly equal to the target values:

impl Game {
    pub fn maxes(&self) -> Round {
        let mut result = Round::default();
        for round in &self.rounds {
            result.red = std::cmp::max(result.red, round.red);
            result.green = std::cmp::max(result.green, round.green);
            result.blue = std::cmp::max(result.blue, round.blue);
        }
        result
    }
}

#[aoc(day2, part1)]
pub fn cube_game(games: &[Game]) -> u32 {
    let mut game_idx = 1;
    let mut result = 0;
    for game in games {
        let maxes = game.maxes();
        if maxes.red <= 12 && maxes.green <= 13 && maxes.blue <= 14 {
            result += game_idx;
        }
        game_idx += 1;
    }
    result
}

For part 2, we must instead determine the minimum number of cubes of each color that could be present in each bag in order for the input game to be possible. Re-using the solution from part 1, this is trivial; the minimum value of each color that would make a game possible is the maximum value seen during any round, which we already have readily available:

#[aoc(day2, part2)]
pub fn cube_power(games: &[Game]) -> u32 {
    games
        .iter()
        .map(|g| {
            let maxes = g.maxes();
            maxes.red * maxes.green * maxes.blue
        })
        .sum()
}

Unlike day 1, the time in day 2 was spent almost entirely in parsing. Running the actual solutions after parsing the Game structs took only 421ns and 407ns respectively. Otherwise, there isn’t too much to say about this one: represent the problem efficiently and you won’t have much to worry about. The solution did require a single allocation, but only during input processing. The problem solutions themselves do not allocate and fit very easily into L1 cache as a result.

Part 2 is also an interesting demonstration of a situation in which parallelization is not beneficial; the loop is so tight and predictable that making full use a single CPU core is much faster than trying to spread the work across cores. Parallelizing the loop (using rayon) takes the latency up to over 16 microseconds, nearly 50 times slower.

The results:

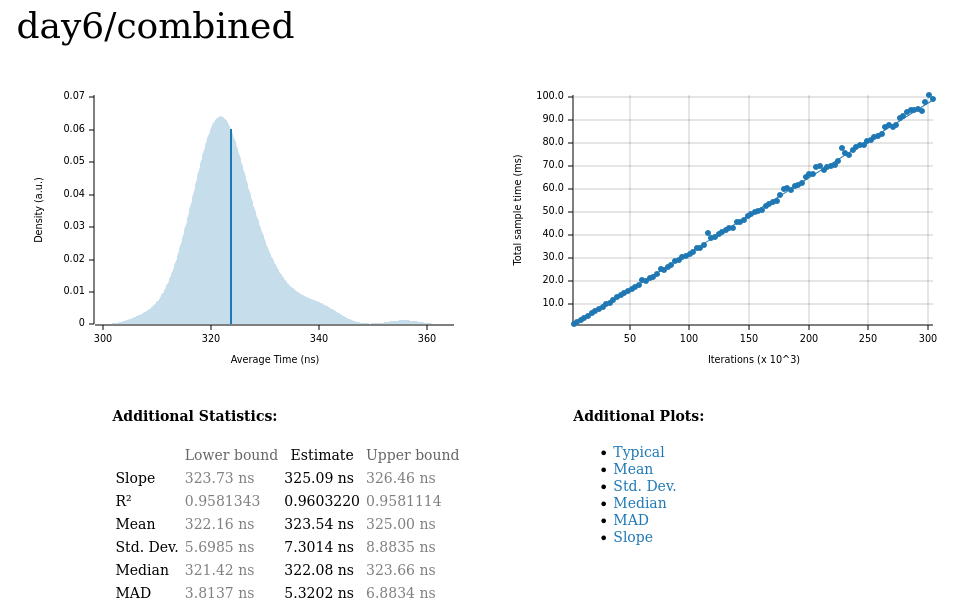
Day 6 🔗

Total input size: negligible
Median latency: 322ns

Solution on GitHub

Day 6 is where things start to get more interesting. The entire solution for both parts including parsing runs in under half of a microsecond! It’s also the first solution where I use a different parsing strategy to solve the two parts of the problem. This is the point where some of the problem statements start to get a bit more complicated, so I’ll do my best to summarize.

The goal for Day 6 is to figure out the number of different ways to win a toy boat race given input that looks like this:

Time:      7  15   30
Distance:  9  40  200

This input shows the results of three different races; one in which 7 meters was traveled in 9ms, one with 15m traveled in 40ms, and one with 30m traveled in 200ms. To participate in the race, you hold down a button which “charges” your boat. Each millisecond that you hold the button gives your boat 1m/ms in additional velocity, but while you’re holding the button the race is still progressing. So, for the first race, there are 4 different ways to win: hold the button for 2, 3, 4, or 5 milliseconds. In the first case, your boat moves at 2m/ms for 5ms, meaning it’s gone 10m - greater than then 9m given in the input.

Parsing for this input is the simplest we’ve seen thus far:

pub type TimeDistancePair = (i64, i64);

#[aoc_generator(day6, part1)]
pub fn generate(input: &str) -> Vec<TimeDistancePair> {
   let (tline, dline) = input.split_once('\n').unwrap();
   let times = tline
       .split_whitespace()
       .skip(1)
       .map(|s| s.parse::<i64>().unwrap());
   let distances = dline
       .split_whitespace()
       .skip(1)
       .map(|s| s.parse::<i64>().unwrap());
   times.zip(distances).collect()
}

Each race is represented by a TimeDistancePair that indicates the total amount of time we have and the minimum distance that must be traveled in order to win. Using this representation, counting the number of wins for each race can be found by realizing that the result is always symmetric about a center point; that is, if holding the button for n milliseconds results in a win, then holding the button for total_time - n milliseconds is guaranteed to also be a win. Similarly, if this relation does not hold, then it’s guaranteed that neither n nor its “complement” result in a win.

Armed with this understanding, we can essentially binary search against the target distance given the max time boundary. When the low end of the search crosses the high end, the number of possible wins can be calculated directly:

fn ways_to_win(time: i64, distance: i64) -> i64 {
    let mut lo = 0;
    let mut hi = time / 2 + (time & 1);
    while lo != hi - 1 {
        let next = (lo + hi) / 2;
        if next * (time - next) > distance {
            hi = next;
        } else {
            lo = next;
        }
    }
    time - hi * 2 + 1
}

#[aoc(day6, part1)]
pub fn race(input: &[TimeDistancePair]) -> i64 {
    let mut result = 1;
    for (time, distance) in input {
        result *= ways_to_win(*time, *distance);
    }
    result
}

I thought this was a very cool solution when I realized it would work. There’s a simple elegance to applying a binary search to a discrete time space like this, and it’s a small, easy to understand implementation to boot. There’s another minor performance trick buried in the implementation on the second line: the starting “high” value for the search needs to differ depending upon whether the target time is even or odd. A bitwise and is the fastest way to extract this information, and makes it easy to express the starting value directly.

Part 2 is a bit of a trick; the input now has to be reinterpreted. Rather than multiple smaller races, the input should be interpreted as one long race by ignoring all white space. This means the input above would now be interpreted as:

Time:      71530
Distance:  940200

After re-parsing, the part 1 solution can be applied directly:

#[aoc_generator(day6, part2)]
pub fn generate_kerning(input: &str) -> TimeDistancePair {
    let (tline, dline) = input.split_once('\n').unwrap();
    let time = tline
        .chars()
        .skip_while(|c| *c != ' ')
        .filter(|c| *c != ' ')
        .collect::<String>()
        .parse::<i64>()
        .unwrap();
    let distance = dline
        .chars()
        .skip_while(|c| *c != ' ')
        .filter(|c| *c != ' ')
        .collect::<String>()
        .parse::<i64>()
        .unwrap();
    (time, distance)
}

#[aoc(day6, part2)]
pub fn race_kerning(input: &TimeDistancePair) -> i64 {
    ways_to_win(input.0, input.1)
}

This demonstrates another important idea behind generating performant solutions to these types of problems. Looking for relationships that can be exploited and fully understanding how the problem works can be more important than writing the code. Thinking about the problem means that less code can be written and that the solution is much faster than a direct implementation. Of course, this may not be an effective approach for landing on the leader board. That being said, implementation of a direct iterative solution may have taken a very long time to run for the second part given the significant increase in the problem size.

It’s worth noting that this problem can also be solved directly using the quadratic equation, but this isn’t something that I realized when I was solving the problem myself. Interestingly, the direct mathematical solution isn’t much faster than this one, though it does have a slight edge when implemented well.

The results:

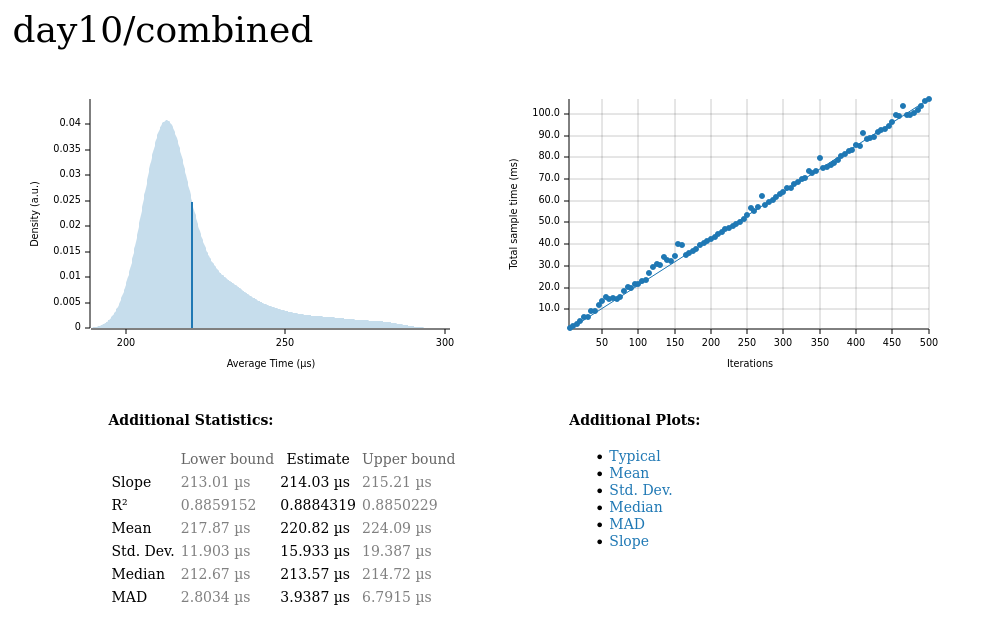
Day 10 🔗

Total input size: 19,740 characters
Median latency: 213μs

Solution on GitHub

Day 10 was the first day that I had to start to look up algorithms that I wasn’t previously familiar with. At least for me, this is a common theme of AOC solutions, and part of the reason that I like to solve these problems. There are so many specific algorithms that I’ve never had the occasion to use professionally, and having an excuse to implement them really helps with understanding and retention. My goal isn’t to be able to implement any of these algorithms by heart, but rather to know that they exist and what their applications are in the event that I come across a “real world” problem that could be solved by applying them.

This day’s problem consists of analysis of a system of pipes. Pipes are represented by characters that show connections between neighboring tiles in a grid, like so:

.....
.F-7.
.|.|.
.L-J.
.....

. characters are “open” tiles, while others hold a specific type of pipe. The pipes that you’re meant to analyze are guaranteed to be connected in a loop that does not branch (though the problem statement never guarantees this). The actual pipes to be traversed by the problem are much more complex. A slightly more realistic example looks like:

7-F7-
.FJ|7
SJLL7
|F--J
LJ.LJ

Notice that not all pipes are connected to the starting position (S)! The actual input to solve is much larger, a 140x140 grid of pipes.

Day 10’s solution in unique in that I solved both parts using a single pass through the input data, so I’ll explain both parts of the problem before presenting any of the code for either solution.

Part 1 asks a relatively straightforward question:

How many steps along the loop does it take to get from the starting position to the point farthest from the starting position?

Because it’s guaranteed that the loop is connected and never branches, we’ll be able to solve this by traversing the pipe and dividing the total path length by 2. Once again this is similar to the intuition used in day 6 to simplify the solution - there’s no need for complicated calculations if we can rely on invariants set within the problem itself.

Part 2, however, makes things much more complicated:

How many tiles are enclosed by the loop?

Much of the complexity of part 2 comes from the complex nature of the loop, and the fact that neighboring tiles may have no space between them at all. For example, in the following diagram, tiles marked I are enclosed by the loop, while those marked O are not enclosed because they have a “path” to the outside of the loop in between columns 4 and 5:

..........
.S------7.
.|F----7|.
.||OOOO||.
.||OOOO||.
.|L-7F-J|.
.|II||II|.
.L--JL--J.
..........

I spent longer than I would like to admit thinking about this problem before I decided to do some research, eventually learning about the nonzero-rule linked from the point in polygon article. This was one of the instances in which ChatGPT was massively helpful; I asked it the following question:

What’s an algorithm/formula that can be used to find the number of points included within a bounding curve?

It recommended an algorithm called ray casting, including a link to the point in polygon Wikipedia page. Given my solution to part 1, it was then immediately obvious how the nonzero rule could be applied to solve the problem easily. This is also the first problem in which I relied upon a property of my specific input in my solution; my starting point was a 7, so I assumed that S could be replaced by 7, which is very likely not true in the general case.

Let’s take a look at the code, starting with the data structures that I used to represent the problem as this representation does most of the heavy lifting.

use crate::util::Res;

// Position update, new direction, winding designator
pub type Connection = (isize, usize, isize);

pub struct PipeMap {
    pipes: Vec<isize>,
    // Up, right, down, left
    connections: [[Connection; 7]; 4],
    start: isize,
}

fn char_to_pipe(c: char) -> isize {
    match c {
        '.' => 0,
        '-' => 1,
        '|' => 2,
        'F' => 3,
        'L' => 4,
        'J' => 5,
        '7' => 6,
        'S' => 7,
        _ => panic!("Invalid pipe char"),
    }
}

Both parts are represented as a single PipeMap. The grid is stored within a single contiguous Vec. Because of the way that pipe connections work, there’s no need to store the actual pipes as a multidimensional grid; rather, the connections directly encode the relationship between the pipes. The char_to_pipe function gives a hint as to how this works: by keeping track of the direction in which the pipe is being traversed, the next position in the vector can be statically encoded by a (direction, type) tuple. This is also why the nonzero-rule is such a good fit to solve this problem: we already have access to the direction of movement and thus the winding direction at each corner.

To clarify a bit further, consider again the simple example given originally (with the 7 in the top left replaced by the starting point):

.....
.F-S.
.|.|.
.L-J.
.....

We have 5 rows and 5 columns. The vector representing this map is just a flattened version of the grid:

......F-S..|.|..L-J......

The column length is the only thing that we need to traverse the flattened grid.

The traversal will start moving to the right, which means we’re using connection index 1. The current pipe type is 7, meaning we’re using type index 6. The update that we need to make is thus connections[1][6]. Moving to the right into the starting point, we must next move “down” one row, which is equivalent to incrementing the current position by the column length. You can verify this for yourself visually: the starting position is at index 8, the column length is 5, and the next position that we have to move to is at index 13. To track the winding, each connection also contains a “winding designator” that can be used to incrementally track whether tiles are inside or outside of the contiguous pipe’s bounding curve. For this step, the connection therefore is (len, 2, -1). Our position needs to be updated by len, our direction needs to be changed to be moving down (index 2), and the winding designator is -1.

Bringing all of this together for the complete input, this is how the PipeMap is parsed:

#[aoc_generator(day10)]
pub fn generate(input: &str) -> PipeMap {
    let len: isize = input.find('\n').unwrap().try_into().unwrap();
    let mut start = 0;
    let pipes: Vec<isize> = input
        .chars()
        .filter(|c| *c != '\n')
        .enumerate()
        .map(|(i, c)| {
            if c == 'S' {
                start = i;
            }
            char_to_pipe(c)
        })
        .collect();
    let connections = [
        [
            (0, 0, 0),
            (0, 0, 0),
            (-len, 0, 1),
            (1, 1, 1),
            (0, 0, 0),
            (0, 0, 0),
            (-1, 3, 1),
        ],
        [
            (0, 0, 0),
            (1, 1, 2),
            (0, 0, 0),
            (0, 0, 0),
            (0, 0, 0),
            (-len, 0, 2),
            (len, 2, -1),
        ],
        [
            (0, 0, 0),
            (0, 0, 0),
            (len, 2, -1),
            (0, 0, 0),
            (1, 1, 2),
            (-1, 3, 2),
            (0, 0, 0),
        ],
        [
            (0, 0, 0),
            (-1, 3, 2),
            (0, 0, 0),
            (len, 2, -1),
            (-len, 0, 2),
            (0, 0, 0),
            (0, 0, 0),
        ],
    ];
    PipeMap {
        pipes,
        connections,
        start: start.try_into().unwrap(),
    }
}

The connections are essentially a “rule table” that is encoded using no allocation and a statically known size. The position updates need to be made in terms of the column length, so the array can’t be const. If you examine the encoded connections, you should be able to discern the symmetry contained within; you can verify for yourself that each “step” will result in the correct update to the current position.

Armed with the primed connection rules, the difficult part is already done. Solving both parts of the problem is now just a matter of applying the rules and interpreting the result:

#[aoc(day10, part1)]
pub fn furthest_pipe(input: &PipeMap) -> Res {
    let mut count = 1;
    let mut curr_pos = input.start + 1;
    let mut curr_dir = 1;
    let mut winding = vec![0; input.pipes.len()];
    while curr_pos != input.start {
        let (pos, dir, wind) = input.connections[curr_dir][input.pipes[curr_pos as usize] as usize];
        winding[curr_pos as usize] = wind;
        curr_pos += pos;
        curr_dir = dir;
        count += 1;
    }

    winding[curr_pos as usize] = 1;
    let mut enclosed = 0;
    let mut wound = 0;
    for wind in winding {
        if wind == 2 {
            continue;
        } else if wind == 0 {
            if wound != 0 {
                enclosed += 1;
            }
        } else {
            wound += wind;
        }
    }

    Res(count / 2, enclosed)
}

The traversal of the pipe for part 1 (and to determine the correct winding designators) is completed with no branches other than the while to detect when traversal is complete. Everything operates on contiguous memory that fits comfortably within L1 cache and is not subject to branch misprediction. After the traversal is complete, a second pass through the winding designators is necessary to calculate the number of tiles enclosed within the pipe. There’s a decent amount of branching here, but application of the nonzero-rule requires this.

Traversing the pipe without any conditional logic is the key to the good performance of this solution. Application of a purpose-built algorithm (the nonzero-rule) greatly simplifies what would otherwise be very complex (and slow) logic to attempt to traverse the entire graph to determine the enclosed tiles.

The results:

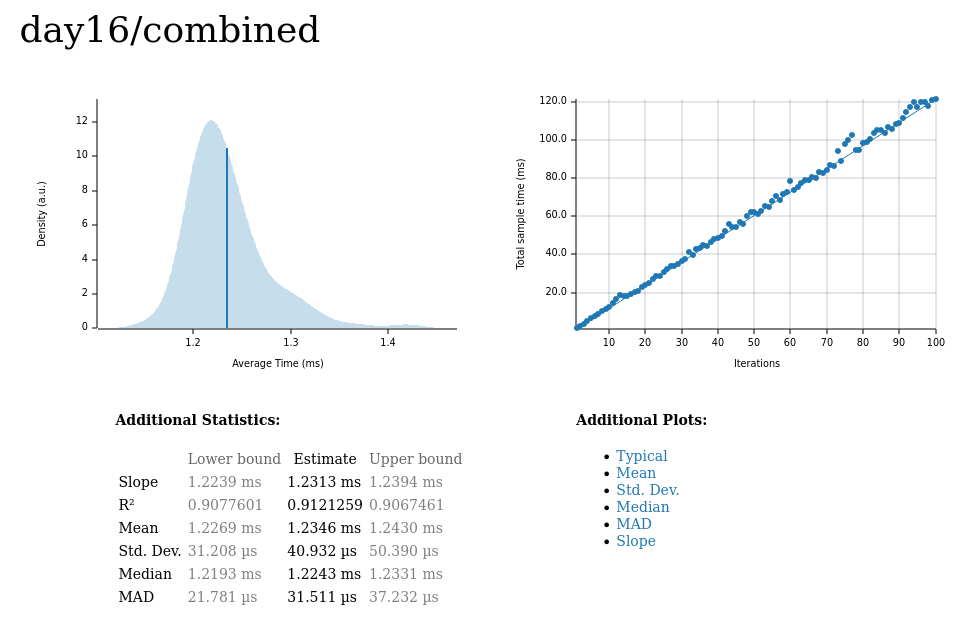
Day 16 🔗

Total input size: 12,200 characters
Median latency: 1.22ms

Solution on GitHub

Day 16 is the final solution I’m going to present. Despite being the slowest solution presented by almost an order of magnitude, this was my favorite problem of the year and the one that I’m happiest with my solution to. As usual, problems get more complicated the further into AOC we go, so I’ll do my best to explain the problem succinctly.

We’re concerned with a grid of mirrors and splitters, like so:

.|...\....
|.-.\.....
.....|-...
........|.
..........
.........\
..../.\\..
.-.-/..|..
.|....-|.\
..//.|....

Light will enter the grid at (0, 0) traveling to the right. If it hits a splitter (| or -) perpendicularly, light is emitted out of both ends of the splitter. If it hits a mirror (/ or \), it will be reflected 90 degrees depending upon the mirror’s orientation and the direction that the light was originally traveling. For example, light traveling to the right that hits a / mirror will be reflected 90 degrees so that it’s now traveling upwards. Hitting a \ mirror would instead reflect downwards. Hitting an empty space (.) or a splitter from a parallel direction does nothing; the light continues to travel in a straight line. The light doesn’t interact with itself, so beams can freely pass through one another. When light encounters the boundary of the grid, it stops and is no longer propagated.

Part 1 requires finding the number of tiles that light passes through. For the example given above, the path of the light looks like:

>|<<<\....
|v-.\^....
.v...|->>>
.v...v^.|.
.v...v^...
.v...v^..\
.v../2\\..
<->-/vv|..
.|<<<2-|.\
.v//.|.v..

This means that the following 46 tiles have light pass through them:

######....
.#...#....
.#...#####
.#...##...
.#...##...
.#...##...
.#..####..
########..
.#######..
.#...#.#..

Similar to day 10, let’s begin with an examination of the data structure used to represent the problem:

#[derive(Clone)]
pub struct Traversal {
    layout: Vec<u8>,
    rows: usize,
    cols: usize,
}

This is it - that’s enough to hold all of the state required to solve part 1! Once again, a realization of properties of the problem input gives the insight required to understand the trick. The problem is asking to track only whether each tile was hit by light or not. This can be determined by encoding the 5 different tile types (3 bits) and the 4 possible traversal directions as a bitmask (4 bits). 3 bits for the types and 4 for the directions is 7 total bits, so we can pack everything that we need into a single u8 for each tile by making use of masks. As with the previous solution, we’re using the “trick” of storing the grid as a contiguous vector rather than a multidimensional structure. If any of the directional traversal bits are set, we know that the tile has been lit, so that information doesn’t need to be stored explicitly.

The rows and cols are needed to detect and handle the boundary conditions, but 128 bits is a small price to pay for the compact tile representation that this provides.

To understand why such a compact representation like this is so important, you need at least a basic understanding of alignment and the hardware cache. A much more thorough discussion of these topics can be found in Drepper’s paper on CPU memory (PDF link). On most processors, a total of 64Kb of memory is available to the L1 cache. Once that amount of memory is exceeded, we’re forced to fall back to L2 cache, resulting in a significant slowdown. With 12,200 tiles to manage, we either have a maximum of 5 bytes per tile to store, or we need to use a sparse representation of the grid in order to stay within L1 cache. Because of how padding and alignment works, even storing a single u32 and a bool would use 8 bytes per tile, taking us out of L1 cache range. So, while there’s a bit of breathing room, representing the entire grid using only a byte per tile more or less guarantees that we will not exceed L1 cache.

First, the parser and the bitmasks that we’ll need:

const UP: u8 = 1;
const RIGHT: u8 = 2;
const DOWN: u8 = 4;
const LEFT: u8 = 8;

const SPLITTER_HORIZ: u8 = 0;
const SPLITTER_VERT: u8 = 1;
const MIRROR_FWD: u8 = 2;
const MIRROR_BWD: u8 = 3;
const OPEN: u8 = 4;

#[aoc_generator(day16)]
pub fn generate(input: &str) -> Traversal {
    let cols = input.find('\n').unwrap();
    let rows = input.len() / cols;
    let layout = input
        .as_bytes()
        .iter()
        .filter(|b| **b != b'\n')
        .map(|b| match *b {
            b'-' => SPLITTER_HORIZ,
            b'|' => SPLITTER_VERT,
            b'/' => MIRROR_FWD,
            b'\\' => MIRROR_BWD,
            b'.' => OPEN,
            _ => panic!("Invalid elem"),
        })
        .collect();

    Traversal { layout, rows, cols }
}

Because the visitation status all start as false (represented by 0 bits), the only processing that we need is to ensure that each tile type is represented properly. The bottom 4 bits are used are used for the type, so they can be parsed as simple u8 values.

The compact byte representation is then paired with a recursive dynamic programming approach. To track all of the light that traverses the mirrors, we follow these basic steps:

1. Start tracking the number of lit tiles at 0
2. Extract all relevant information from the packed byte: the tile type and whether the tile has been visited from each direction
3. If the tile has been visited from the current traversal direction, return the number of lit tiles tracked thus far
4. Otherwise, if this is the first time the tile is being visited, increment the number of lit tiles
5. Set the bit denoting that the tile has been visited from the current direction
6. Use the tile type and the current direction to determine the subsequent location(s) and direction(s) (there can be multiple because of splitters)
7. Recurse on each subsequent traversal

Given this, the part 1 solution:

impl Traversal {
    pub fn energized(&mut self) -> usize {
        self.traverse(0, 0, RIGHT)
    }

    #[inline(always)]
    fn idx(&self, row: usize, col: usize) -> usize {
        row * self.cols + col
    }

    fn step(&self, row: usize, col: usize, dir: u8) -> Option<(usize, usize)> {
        match dir {
            UP if row == 0 => None,
            UP => Some((row - 1, col)),
            RIGHT if col == self.cols - 1 => None,
            RIGHT => Some((row, col + 1)),
            DOWN if row == self.rows - 1 => None,
            DOWN => Some((row + 1, col)),
            LEFT if col == 0 => None,
            LEFT => Some((row, col - 1)),
            _ => panic!("Invalid direction"),
        }
    }

    pub fn traverse(&mut self, mut row: usize, mut col: usize, mut dir: u8) -> usize {
        let mut energized = 0;
        loop {
            let idx = self.idx(row, col);
            let curr = self.layout[idx] & 0xF;
            let visited = self.layout[idx] >> 4;
            if dir & visited != 0 {
                break;
            }
            if visited == 0 {
                energized += 1;
            }
            self.layout[idx] |= dir << 4;
            match curr {
                SPLITTER_HORIZ => {
                    if dir == UP || dir == DOWN {
                        if let Some((r, c)) = self.step(row, col, LEFT) {
                            energized += self.traverse(r, c, LEFT);
                        }
                        dir = RIGHT;
                    }
                }
                SPLITTER_VERT => {
                    if dir == LEFT || dir == RIGHT {
                        if let Some((r, c)) = self.step(row, col, UP) {
                            energized += self.traverse(r, c, UP);
                        }
                        dir = DOWN;
                    }
                }
                MIRROR_FWD => match dir {
                    UP => dir = RIGHT,
                    RIGHT => dir = UP,
                    DOWN => dir = LEFT,
                    LEFT => dir = DOWN,
                    _ => panic!("Invalid dir"),
                },
                MIRROR_BWD => match dir {
                    UP => dir = LEFT,
                    RIGHT => dir = DOWN,
                    DOWN => dir = RIGHT,
                    LEFT => dir = UP,
                    _ => panic!("Invalid dir"),
                },
                _ => {}
            }
            if let Some((r, c)) = self.step(row, col, dir) {
                row = r;
                col = c;
            } else {
                break;
            }
        }
        energized
    }
}

#[aoc(day16, part1)]
pub fn mirror_energy(input: &Traversal) -> usize {
    input.clone().energized()
}

The bit twiddling is not too complicated. The bottom 4 bits store the type, while the top 4 store the directional visitation status. The relevant operations can be found in the first ~10 lines of the traverse function:

• self.layout[idx] & 0xF: extract the type from the current position by masking it with 1111
• self.layout[idx] >> 4: extract the visitation status from the current position by shifting the top 4 bits into the bottom 4 bits
• dir & visited != 0: because dir is a mask, this tells us whether the visitation status is set for the current direction
• self.layout[idx] |= dir << 4: set the visitation status to true for the current direction. The mask is left shifted 4 bits before being applied so that it applies to the top bits only

The rest of the implementation simply follows the steps given above.

Part 2 extends the problem to ask: instead of starting at (0, 0) and moving to the right, if the light could instead start in any border tile, what’s the maximum possible number of tiles that will be lit? Light entering from corner tiles can start in either direction and these two possibilities should be treated independently.

Because of the speed of the part 1 solution, a simple brute force approach solves part 2 trivially:

use rayon::prelude::{IntoParallelRefIterator, ParallelIterator};

#[aoc(day16, part2)]
pub fn max_mirror_energy(input: &Traversal) -> usize {
    let mut traversals = Vec::with_capacity(500);
    for r in 0..input.rows {
        traversals.push((r, 0, RIGHT));
        traversals.push((r, input.cols - 1, LEFT));
    }
    for c in 0..input.cols {
        traversals.push((0, c, DOWN));
        traversals.push((input.rows - 1, c, UP));
    }
    traversals
        .par_iter()
        .map(|(r, c, d)| input.clone().traverse(*r, *c, *d))
        .max()
        .unwrap()
}

Rayon allows for naive parallelization of the problem through the use of a parallel iterator (par_iter). While it is possible to answer the question without traversing every possibility (because light leaving through a tile is guaranteed to light the same number of tiles as light entering from that tile), reducing the search space in this way requires waiting on previous iterations to complete, which slows down the overall solution despite theoretically doing less work.

The results:

Wrapping up 🔗

I had a lot of fun with AOC again this year. Hopefully these solutions gave you some insight into a few strategies that you can use to generate these types of low-latency solutions. All of my solutions are available in the GitHub repository; if you’d like an explanation for one of the days that I haven’t highlighted in this post, please drop me an issue and I’ll be happy to add it.